...megvan az adattömb, lássuk az ornátust! Azaz ábrázoljuk az árut a lehető legbénább módon, viszont gyorsan.
Col <- with(LongSubData,ifelse(Type=="n","red","blue"))
Pch <- with(LongSubData,ifelse(time=="Before",21,19))
plot(Weight~Days,col=Col,pch=Pch,data=LongSubData,cex.axis=2,cex.lab=2,cex=2)
legend("topleft",legend=c("Pucéran","Ruhában etetés előtt","Ruhában etetés után"),
pch=c(21,21,19),col=c("red","blue","blue"),cex=2)
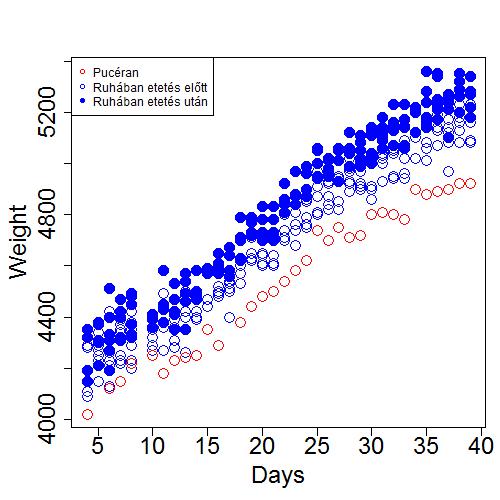
Minden növekedési görbéről tudvalevő – ok, a legtöbbről - hogy valamilyen felső határértékhez tart. (Szépemlékű irodalom tanárnőm állítása szerint ez a jelenség tántorította el a matematikától – folyamatosan közelíti, de soha el nem éri…az meg hogy lehet, he?). Ebben az esetben ezt zárójelbe tenném és azt feltételezném, hogy bár ismerjük e jelenséget, az adatok ezen a ponton még nem teszik lehetővé a korrekt aszimptotikus illesztést. Értsd; az adathalmaz lehetővé tesz ugyan ilyen illesztést, de úgyse hinnénk el mert ezek matematikai modellek, nem gondolkodnak csak illeszkednek – ha kell ha nem… Nekünk kell gondolkodni. Milyen szomorú! Maradjunk egyenlőre csak a lineáris közelítéseknél, azok olyan biztonságosak.
Kiindulásként három szisztematikus hatást feltételezek – ehhez nem is kell sok fantázia. Az idő előrehaladtával a súly nyilván növekszik, ha ruhában van az növeli a súlyt ha eszik az is. A lineáris modell a következőképpen néz ki:
lm01 <- lm(Weight~Days+time+Type,data=LongSubData)
> summary(lm01)
Call:
lm(formula = Weight ~ Days + time + Type, data = LongSubData)
Residuals:
Min 1Q Median 3Q Max
-195.760 -52.532 -3.697 47.737 185.315
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3975.5414 16.0212 248.14 <2e-16 ***
Days 29.9103 0.3309 90.39 <2e-16 ***
timeBefore -101.7033 7.3169 -13.90 <2e-16 ***
Types 181.3852 13.2069 13.73 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 69.8 on 393 degrees of freedom
Multiple R-squared: 0.9566, Adjusted R-squared: 0.9563
F-statistic: 2888 on 3 and 393 DF, p-value: < 2.2e-16
Bika kis modell mi? Lássuk mit is mond!
A gyerek 3976 g-al született…majdnem stimmel 4116 g volt. Az illesztett időszakban naponta 30 g-ot gyarapodott. A ráadott ruha súlya átlag 181 g-ot nyomott (nem páncélinget adtunk rá), valamint az etetések során 101 ml –t evett (hát nem teljesen…). Ezek mind olyan számok amik majdnem hihetőek, az egyetlen gyanús darab az a 70g-os RSE. Ez ha minden ok lenne a modellel a mérési hibát kéne hogy jelentse. Nem vagyok 100%-ig elégedett a termékkel de a legrosszabb időszakaiban is maximum a harmada volt ennek a hiba.
Mi lehet a baj? Több ötletem is van.
A gyerek napi súlyváltozása elméletileg inkább így néz ki
Vagyis van egy napon belüli ritmusa a testsúlyingadozásnak. Ez már önmagában is jelentős nem magyarázott varianciát jelent. Kár hogy a mérések mellé rendelt sorszámok csak durva időfelbontást tennének lehetővé, plusz most csak lineáris modellekkel operálunk.
Van ezenfelül egy másik valószínű jelenség, ez pedig a megevett mennyiség változása az időben. Ez egy picit a feje tetejére fordul itt, mert a modellben ez úgy jelentkezne, hogy más meredekséget rendelünk az idő faktor mellé etetett és nem etetett esetben. Így ni:
lm02 <- lm(Weight~Days*time+Type,data=LongSubData)
>summary(lm02)
Call:
lm(formula = Weight ~ Days * time + Type, data = LongSubData)
Residuals:
Min 1Q Median 3Q Max
-191.014 -49.101 -4.072 48.986 187.967
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3956.1589 17.6821 223.738 < 2e-16 ***
Days 30.8026 0.4837 63.684 < 2e-16 ***
timeBefore -65.0842 16.2752 -3.999 7.6e-05 ***
Types 181.0582 13.1190 13.801 < 2e-16 ***
Days:timeBefore -1.6579 0.6593 -2.515 0.0123 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 69.33 on 392 degrees of freedom
Multiple R-squared: 0.9573, Adjusted R-squared: 0.9569
F-statistic: 2197 on 4 and 392 DF, p-value: < 2.2e-16
Na, ettől jobb is lett a modell.
Ennek bizonyítására összehasonlítom a két modellt.
> anova(lm01,lm02)
Analysis of Variance Table
Model 1: Weight ~ Days + time + Type
Model 2: Weight ~ Days * time + Type
Res.Df RSS Df Sum of Sq F Pr(>F)
1 393 1914670
2 392 1884274 1 30396 6.3235 0.01231 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Szóval ez a modell pont annyival jobb, mint amennyit az interakció hozzátesz (de meglepő…).
Az új modell szerint 3956 grammal született. A ruha még mindig 181 gramm DE, eleinte 65 mili körül eszik és ez minden nappal 1,6 milivel nő. Nem mondom hogy tökéletes, de egynek jó lesz.
Lássuk hogy grafikusan milyen az illesztett modell.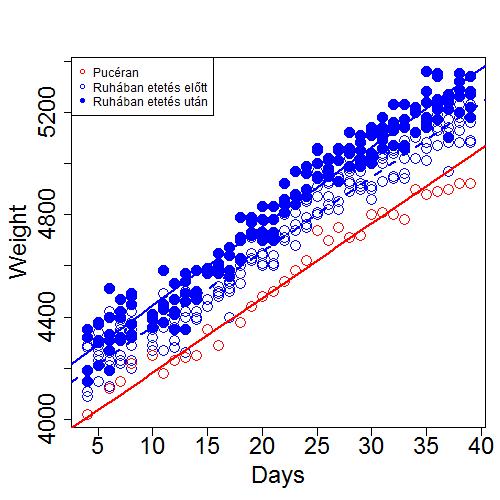
Csudás...
